Random Triangles

Suppose that a stick is randomly broken in two places. What is the probability that the three pieces form a triangle?

Without looking below, make a guess.

Run the triangle experiment 50 times. Do not be concerned with all of the information displayed in the app, but just note whether the pieces form a triangle. Would you like to revise your guess?

Mathematical Formulation

As usual, the first step is to model the random experiment mathematically. We will take the length of the stick as our unit of length, so that we can identify the stick with the interval

[0, 1]

. To break the stick into three pieces, we just need to select two points in the interval. Thus, let

X

denote the first point chosen and

Y

the second point chosen. Note that

X

and

Y

are random variables and so the sample space of our experiment is

(S, S)

where

S = [0, 1]^{2}

and

S

is the standard collection of subsets of

S

. Now, to model the statement that the points are chosen at random, let us assume, as in the previous sections, that

X

and

Y

are independent and each is uniformly distributed on

[0, 1]

The random point $(X, Y)$ is uniformly distributed on $S = [0, 1]^{2}$ and hence $P [(X, Y) \in A] = \frac{area (A)}{area (S)}, A \in S$

Triangles

The Probability of a Triangle

The three pieces form a triangle if and only if the triangle inequalities hold: the sum of the lengths of any two pieces must be greater than the length of the third piece.

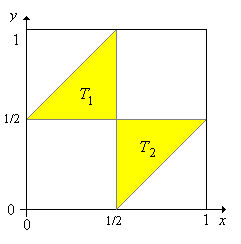
The event that the pieces form a triangle is $T_{1} \cup T_{2}$ where

$T_{1} = {(x, y) \in S : y > \frac{1}{2}, x < \frac{1}{2}, y - x < \frac{1}{2}}$
$T_{2} = {(x, y) \in S : x > \frac{1}{2}, y < \frac{1}{2}, x - y < \frac{1}{2}}$

A sketch of the event

T

is given below. Curiously,

T

is composed of triangles!

The probability that the pieces form a triangle is $P (T) = \frac{1}{4}$ .

How close did you come with your initial guess? The relative low value of

P (T)

is a bit surprising.

Run the triangle experiment 1000 times and compare the empirical probability of $T^{c}$ to the true probability.

Triangles of Different Types

Now let us compute the probability that the pieces form a triangle of a given type. Recall that in an acute triangle all three angles are less than 90°, while an obtuse triangle has one angle (and only one) that is greater than 90°. A right triangle, of course, has one 90° angle.

Suppose that a triangle has side lengths $a$ , $b$ , and $c$ , where $c$ is the largest of these. The triangle is

acute if and only if $c^{2} < a^{2} + b^{2}$ .
obtuse if and only if $c^{2} > a^{2} + b^{2}$ .
right if and only if $c^{2} = a^{2} + b^{2}$ .

Part (c), of course, is the famous Pythagorean theorem, named for the ancient Greek mathematician Pythagoras.

The right triangle equations for the stick pieces are

$(y - x)^{2} = x^{2} + (1 - y)^{2}$ in $T_{1}$
$(1 - x)^{2} = x^{2} + (y - x)^{2}$ in $T_{1}$
$x^{2} = (y - x)^{2} + (1 - y)^{2}$ in $T_{1}$
$(x - y)^{2} = y^{2} + (1 - x)^{2}$ in $T_{2}$
$(1 - x)^{2} = y^{2} + (x - y)^{2}$ in $T_{2}$
$y^{2} = (x - y)^{2} + (1 - x)^{2}$ in $T_{2}$

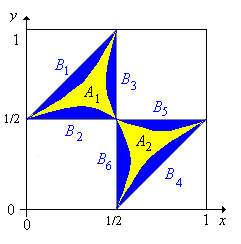
Let $R$ denote the event that the pieces form a right triangle. Then $P (R) = 0$ .

The event that the pieces form an acute triangle is $A = A_{1} \cup A_{2}$ where

$A_{1}$ is the region inside curves (a), (b), and (c) of the right triangle equations in [9].
$A_{2}$ is the region inside curves (d), (e), and (f) of the right triangle equations in [9].

The event that the pieces form an obtuse triangle is $B = B_{1} \cup B_{2} \cup B_{3} \cup B_{4} \cup B_{5} \cup B_{6}$ where

$B_{1}$ , $B_{2}$ , and $B_{3}$ are the regions inside $T_{1}$ and outside of curves (a), (b), and (c) of the right triangle equations in [9], respectively.
$B_{4}$ , $B_{5}$ , and $B_{6}$ are the regions inside $T_{2}$ and outside of curves (d), (e), and (f) of the right triangle equations in [9], respectively.

The probability that the pieces form an obtuse triangle is $P (B) = \frac{9}{4} - 3 \ln (2) \approx 0.1706$

Details:

Simple calculus shows that $P (B_{i}) = 3 / 8 - \ln (2) / 2$ for each $i \in {1, 2, 3, 4, 5, 6}$ . For example $\begin{aligned} P (B_{1}) & = \int_{0}^{1 / 2} \frac{x (1 - 2 x)}{2 - 2 x} d x \\ P (B_{3}) & = \int_{0}^{1 / 2} (y + \frac{1}{2 y} - \frac{3}{2}) d y \end{aligned}$ From symmetry it also follows that $P (B_{i})$ is the same for each $i$ .

The probability that the pieces form an acute triangle is $P (A) = 3 \ln (2) - 2 \approx 0.07944$

Details:

Note that $A \cup B \cup R = T$ , and $A$ , $B$ , and $R$ are disjoint.

Run the triangle experiment 1000 times and compare the empirical probabilities to the true probabilities.

3. Random Triangles

Preliminaries

Statement of the Problem

Mathematical Formulation

Triangles

The Probability of a Triangle

Triangles of Different Types